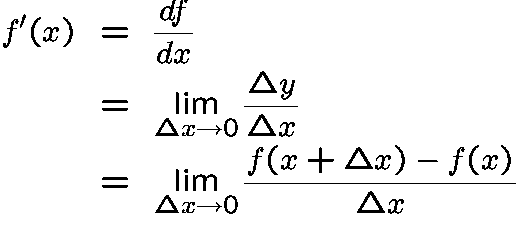
PSYCH3W03/NEURCOMP3W03 Differentiation

Differentiation

The derivative of a function y = f(x) is defined as:

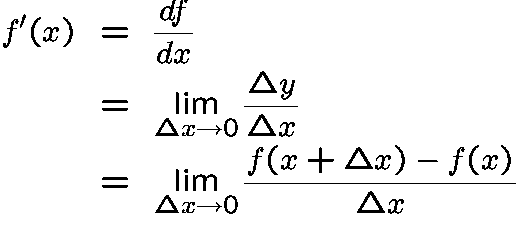
For a linear function y = f(x) = bx + c, the derivative is equal to the slope b. Proof:

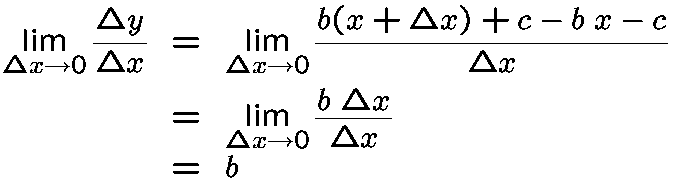
For a quadratic function,

the derivative equals 2ax + b. Proof left as an exercise.

Composite functions

For a composite function, y = f(g(x)), we can apply the chain rule to get f'(x):

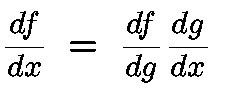
That is, although the argument of f is another function g(x), we treat g(x) as if it were just a regular variable and differentiate f using ordinary differentiation with respect to that variable. We then multiply by the derivative of g with respect to x, or in other words g'(x), to get the complete derivative.

Partial Derivatives

For a function of two (or more) variables, f(x_1, x_2), there is no single derivative but we can talk about the partial derivatives with respect to each variable. These are just the ordinary derivatives of the function with respect to one variable while holding the other variables constant.

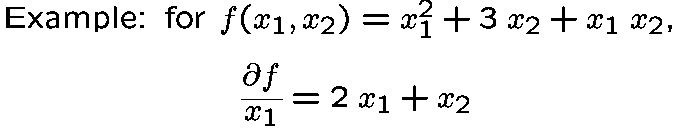
The gradient is defined as the vector of partial derivatives of the function with respect to each variable; i.e. for each variable, we take the derivative of the function with respect to that one variable while treating all the others as constants.